목차
수학 기호 및 그리스 문자 정리
수학에서는 다양한 기호와 문자를 사용하여 복잡한 개념과 연산을 간결하게 표현합니다. 이 글에서는 수학 기호와 그리스 문자들을 정리해보겠습니다. 이러한 기호들은 수학적 사고와 표현의 핵심적인 부분을 담당하며, 수학을 공부하는 데 있어 반드시 이해하고 숙지해야 합니다.


1. 아라비아 숫자와 기수법
- 아라비아 숫자: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- 기수법: 수를 표현하고 기록하는 방법으로, 다양한 진법이 있습니다.
2. 수의 집합
- 자연수: ℕ
- 정수: ℤ
- 유리수: ℚ
- 무리수: ℚc
- 실수: ℝ
- 복소수: ℂ
3. 사칙연산 기호
- 더하기: +
- 빼기: -
- 곱하기: x
- 나누기: ÷
4. 중요한 상수들
- 자연로그의 밑 (e)
- 원주율 (π): 3.141592653589...
- 허수 단위 (i)
5. 변수와 상수
- 변수 (미지수): x, y, z 등
- 상수: a, b, c 등
6. 집합과 관련된 기호
- 속한다: ∈
- 공집합: ∅
- 부분집합: ⊆
- 진부분집합: ⊂
- 합집합: ∪
- 교집합: ∩
- 여집합: Ac
7. 관계 표현 기호
- 상등 (같음): =
- 거의 같음: ≒
- 부정: ≠
- 크다: >
- 작다: <
- 크거나 같다: ≥
- 작거나 같다: ≤
8. 논리 기호
- 모든: ∀
- 존재한다: ∃
- 그리고 (논리곱): ∧
- 또는 (논리합): ∨
- 부정: ¬ 또는 ~
- 조건, 함의: → 또는 ⇒
- 특정 조건을 만족시키는: s.t
9. 증명과 관련된 기호
- 증명의 시작: 보통 '증명'이라는 단어로 시작
- 증명의 마침: Q.E.D, □, ■, ◆ 등
10. 수열, 급수, 극한 기호
- 수열: { }
- 급수 (시그마): ∑
- 곱기호 (파이): ∏
- 무한대: ∞
- 수렴: →
11. 함수와 관련된 기호
- 함수 표현: f: X → Y
- 역함수: f-1
- 합성함수: ∘
- 지수 함수: ex = exp(x)
12. 미분과 관련된 기호
- 증분 (델타 Δ)
- 미분 계수, 도함수: f′(x) = y′ = dy/dx = ˙y = df/dx = ˙f = d/dx f(x) = Df(x) = Dx f(x)
- 편미분 계수: ∂/∂x
13. 적분 기호
- 부정적분: ∫
- 정적분: ∫ab
- 선적분: ∮
이러한 기호들은 수학을 이해하고 표현하는 데 있어 필수적인 요소들입니다. 각 기호가 갖는 의미와 사용법을 숙지하면 수학 문제를 해결하는 데 있어 보다 명확하고 효율적인 방법을 제시할 수 있습니다.
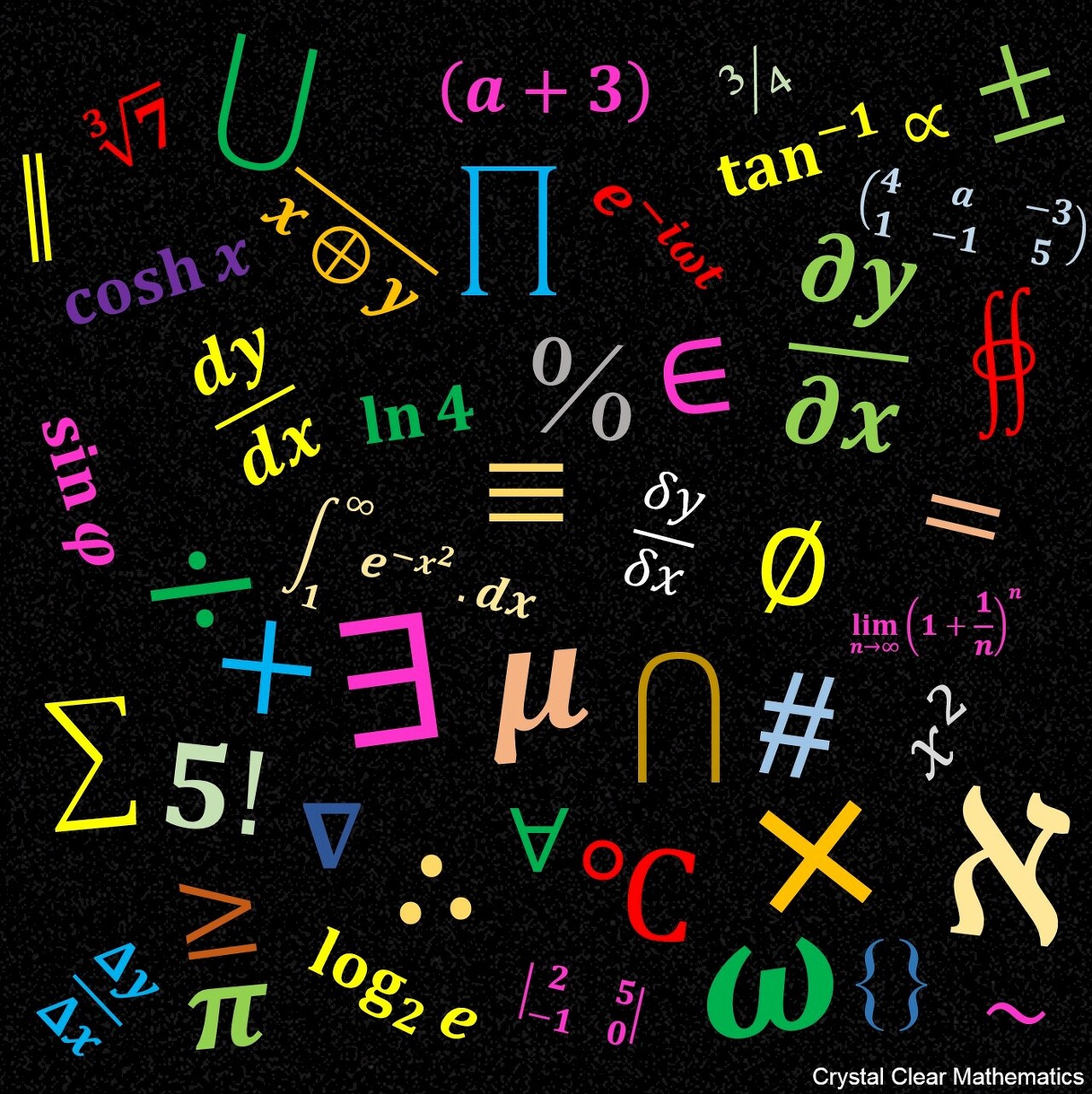
대수 기호와 그 의미
대수학은 수학의 한 분야로, 수와 기호를 사용하여 수학적 연산과 관계를 표현합니다. 이 섹션에서는 대수학에서 자주 사용되는 기호들과 그 의미를 살펴보겠습니다.
1. 기본 변수와 연산 기호
- x (변수): 알려지지 않은 값을 나타냄. 예: 2x = 4 일 때 x = 2
- ≡ (등가): 두 표현이 동일함을 나타냄.
- ≜, : = (정의상 같음): 좌우 항이 정의상 같음을 나타냄.
- ~ (거의 동일): 약한 근사를 나타냄. 예: 11 ~ 10
- ≈ (근사): 두 값이 거의 같음을 나타냄. 예: sin(0.01) ≈ 0.01
- ∝ (비례): 두 변수가 서로 비례함을 나타냄. 예: y ∝ x는 y = kx (k는 상수)를 의미
2. 특수 기호와 그 의미
- ∞ (Lemniscate): 무한대를 나타냄.
- ≪, ≫ (훨씬 적거나 큼): 한 값이 다른 값에 비해 훨씬 작거나 큼을 나타냄. 예: 1 ≪ 1000000, 1000000 ≫ 1
- (), [], {} (괄호류): 수학적 표현의 계산 순서를 구분함. 예: 2 * (3 + 5) = 16, [(1 + 2) * (1 + 5)] = 18
- ⌊x⌋, ⌈x⌉ (바닥/천장 브래킷): 숫자를 하한/상한 정수로 반올림. 예: ⌊4.3⌋ = 4, ⌈4.3⌉ = 5
- x! (팩토리얼): 주어진 숫자까지의 모든 정수의 곱. 예: 4! = 1 * 2 * 3 * 4 = 24
- |x| (절대 값): 숫자의 절대 값을 나타냄. 예: | -5 | = 5
3. 함수와 연산 관련 기호
- f(x) (함수): x의 값을 함수 f(x)에 매핑. 예: f(x) = 3x + 5
- (f ∘ g) (함수 합성): 두 함수의 합성을 나타냄. 예: f(x) = 3x, g(x) = x - 1 ⇒ (f ∘ g)(x) = 3(x - 1)
- (a, b), [a, b] (간격): 개방/폐쇄 간격을 나타냄. 예: x ∈ (2,6), x ∈ [2,6]
- ∆ (델타): 변화나 차이를 나타냄. 예: ∆t = t1 - t0
- ∑ (시그마), ∏ (파이): 합계, 곱셈의 시리즈를 나타냄. 예: Σxi = x1 + x2 + ... + xN, ∏xi = x1 ∙ x2 ∙ ... ∙ xn
- e (오일러 수), γ (오일러-마스케로니 상수), φ (황금비), π (파이 상수): 특정한 수학적 상수를 나타냄.
이러한 기호들은 대수학에서 매우 중요한 역할을 하며, 수학적 개념을 명확하게 전달하는 데 사용됩니다. 대수학을 이해하는 데 있어 이러한 기호와 그 의미를 정확히 아는 것이 필수적입니다.
기본 수학 기호와 그 의미
수학에서 사용되는 다양한 기호들은 특정한 의미를 가지며, 이러한 기호들의 정확한 이해는 수학적 개념을 올바르게 파악하는 데 중요합니다. 아래에서는 기본적인 수학 기호들과 그들의 이름, 의미 및 사용 예시를 살펴보겠습니다.
1. 평등과 불평등 기호
- 등호 (=): 두 값이 같음을 나타냄.
- 예: (5 = 2 + 3) (5는 2와 3의 합과 같습니다)
- 등호가 아님 (≠): 두 값이 같지 않음을 나타냄.
- 예: (5 ≠ 4) (5는 4와 같지 않습니다)
- 거의 동일 (≈): 두 값이 근사적으로 같음을 의미.
- 예: (\sin(0.01) ≈ 0.01)
- 엄격한 불평등 (>): 한 값이 다른 값보다 큼.
- 예: (5 > 4) (5는 4보다 큽니다)
- 엄격한 불평등 (<): 한 값이 다른 값보다 작음.
- 예: (4 < 5) (4는 5보다 작습니다)
- 불평등 (≥): 한 값이 다른 값보다 크거나 같음.
- 예: (4 ≤ 5) (4는 5보다 작거나 같습니다)
2. 연산 기호
- 더하기 기호 (+): 두 수의 합산.
- 예: (1 + 1 = 2)
- 빼기 기호 (−): 한 수에서 다른 수를 빼는 연산.
- 예: (2 - 1 = 1)
- 더하기-빼기 (±): 두 연산을 모두 포함.
- 예: (3 ± 5)는 8 또는 -2를 의미
- 곱셈 기호 (*): 두 수의 곱.
- 예: (2 * 3 = 6)
- 곱셈 점 (⋅): 두 수의 곱.
- 예: (2 ⋅ 3 = 6)
- 나눗셈 기호 (÷): 한 수를 다른 수로 나눔.
- 예: (6 ÷ 2 = 3)
- 나눗셈 슬래시 (/): 한 수를 다른 수로 나눔.
- 예: (6/2 = 3)
3. 고급 수학 연산 기호
- 제곱근 (√): 수의 제곱근.
- 예: (\sqrt{9} = ±3)
- 세제곱근 (3√): 수의 세제곱근.
- 예: (3\sqrt{8} = 2)
- n 번째 뿌리 (n√): 수의 n번째 뿌리.
- 예: (n=3)일 때, (3\sqrt{8} = 2)
4. 기타 기호
- 퍼센트 (%): 백분율.
- 예: (10% × 30 = 3)
- 밀당 (‰): 천분율.
- 예: (10 ‰ × 30 = 0.3)
- ppm (백만 당): 백만 분의 일.
- 예: (10ppm × 30 = 0.0003)
이러한 기호들은 수학적 표현과 계산의 기본이며, 수학을 이해하고 사용하는 데 필수적인 요소입니다. 각 기
호의 정확한 의미를 이해하고 올바르게 사용하는 것은 수학적 문제를 풀고, 실생활에서 수학을 적용하는 데 있어 매우 중요합니다.
수학 기호 표기와 용어의 중요성
수학은 그 자체로 광범위하고 복잡한 학문 분야입니다. 수학적 표기법과 용어는 이러한 복잡성을 간결하고 정확하게 전달하는 데 필수적인 역할을 합니다. 이 부분에서는 수학적 표기법과 용어의 중요성에 대해 더 깊이 탐구해보겠습니다.
1. 수학적 표기법의 역할
- 표준화된 커뮤니케이션: 수학적 표기법은 전 세계 수학자들이 동일한 언어를 사용함으로써 아이디어를 명확하고 효율적으로 교환할 수 있게 합니다.
- 복잡한 개념의 간결한 표현: 연산, 관계, 불특정 수 등을 포함한 복잡한 수학적 개념을 간단하고 명확한 기호로 표현합니다.
2. 기호의 다양성과 사용
- 변수와 상수: 변수는 주로 그리스 문자나 라틴 문자로 표현되며, 수학적 객체의 값을 대표합니다.
- 연산 기호: 더하기(+), 빼기(-), 곱하기(×), 나누기(÷) 등의 기본적인 연산부터 미분(∂), 적분(∫)과 같은 고급 연산까지 다양합니다.
- 그룹화된 기호: 등호(=), 부등호(<, >), 논리 연산자(∧, ∨) 등이 특정 규칙을 따라 사용됩니다.
3. 수학적 용어의 발전과 의미
- 공리와 추측: 공리는 증명 없이 참으로 받아들여지는 가정이며, 추측은 아직 증명되지 않은 가설을 의미합니다.
- 정리와 렌마: 정리는 논리적 추론을 통해 증명된 사실이며, 렌마는 다른 정리를 증명하는 데 사용되는 중간 단계의 정리입니다.
- 관사: 증명된 일반적인 예시나 사례를 의미합니다.
4. 수학 용어의 일상 언어와의 차이
- 단어의 다의성: 예를 들어, 'even'은 수학에서 '짝수'를 의미하지만 일상 언어에서는 '심지어'나 '평평한' 등 다른 의미를 가집니다.
- 전문 용어의 중요성: 수학 용어는 특정 개념을 명확하게 전달하기 위해 고안되었으며, 이러한 용어 없이는 수학적 아이디어를 정확하게 이해하거나 전달하기 어렵습니다.
수학적 표기법과 용어는 수학의 복잡한 아이디어를 전달하는 데 있어 필수적인 수단입니다. 이러한 기호와 용어를 이해하고 숙지하는 것은 수학을 학습하고 의사소통하는 데 있어 매우 중요합니다. 또한, 이러한 지식은 수학적 사고와 문제 해결 능력을 키우는 데 기여하며, 다른 과학 및 공학 분야에서도 그 가치를 발휘합니다.
'어학 어원 상식' 카테고리의 다른 글
| 멋있는 멋진 영어 단어 다국적 기업의 슬로건 뜻 (0) | 2024.02.26 |
|---|---|
| What a Wonderful World 루이 암스트롱 대표곡 (0) | 2024.02.14 |
| 루이 암스트롱 "When the Saints Go Marching In" 가사 해석 (0) | 2024.02.13 |
| SWAT 수신호의 뜻과 전술적 손신호, 핵심 용어 설명 & 스와트 밈 (0) | 2023.08.15 |
| 루이 암스트롱 What a Wonderful World 가사 해석 La Vie en Rose, When The Saints Go Marching In, Hello, Dolly! (0) | 2023.08.04 |




댓글